Contents


Introduction

Numba and Cython promise a lot to speed up this dead slow language called Python. But what to use in production to speed-up numpy array handling? I provided a few similar benchmarks in this talk already. However, the main difference here is, that I’m not benchmarking the math operations itself but also the I/O (the matrix M is returned from the function). Further, I find it quite difficult to use Numba in production code. Due to the nature of a JIT, it may causes a few surprises and the speed-up was not always as good as promised. In other words, I never found numba to be really helpful outside a few Jupyter notebook examples.

Therefore, we’ll have a look NumPy array processing. Using np.sin(M) is considered as “best practice” when applying a mathematical function to every element of an array.

Setup

The setup is straight forward. The following functions are evaluated on numpy arrays of dimensions (1x1), (10x10), (100x100). On larger arrays (1000x1000, 10000x10000) only numba and cython memory functions were evaluated. Each function is evaluated 1000 times on each input array.

def native_python(M):
    """Native Python function to compute
       sin of every element in a NumPy array
    """
    for i in range(M.shape[0]):
        for j in range(M.shape[1]):
            M[i,j] = math.sin(M[i,j])
    return M

def native_numpy(M):
    """Native NumPy function to calculate
       element-wise sin of a NumPy array
    NB!: defined as a function to incorporate 
         function call overhead
    """
    return np.sin(M)

@numba.njit(parallel=False, boundscheck=False)
def native_numba(M):
    """Native Numba accelerated Python function to compute
       sin of every element in a NumPy array
    """
    for i in range(M.shape[0]):
        for j in range(M.shape[1]):
            M[i,j] = math.sin(M[i,j])
    return M

import cython

cimport numpy as np
import numpy as np

DTYPE = np.float

from libc.math cimport sin



@cython.boundscheck(False)
@cython.wraparound(False)
cpdef mixed_cython(M):
    cdef Py_ssize_t dim0 = M.shape[0]
    cdef Py_ssize_t dim1 = M.shape[1]
    cdef Py_ssize_t i,j

    for i in range(dim0):
        for j in range(dim1):
            M[i,j] = sin(M[i,j])
    return M

@cython.boundscheck(False)
@cython.wraparound(False)
cpdef np.ndarray native_cython(np.ndarray M):
    cdef Py_ssize_t dim0 = M.shape[0]
    cdef Py_ssize_t dim1 = M.shape[1]
    cdef Py_ssize_t i,j
    
    assert M.dtype == DTYPE
    
    for i in range(dim0):
        for j in range(dim1):
            M[i,j] = sin(M[i,j])
    
    return M


@cython.boundscheck(False)
@cython.wraparound(False)
cpdef mem_view_cython(double[:, :] M):
    cdef Py_ssize_t dim0 = M.shape[0]
    cdef Py_ssize_t dim1 = M.shape[1]
    cdef Py_ssize_t i,j
    
    for i in range(dim0):
        for j in range(dim1):
            M[i,j] = sin(M[i,j])    

    return M

@cython.boundscheck(False)
@cython.wraparound(False)
cpdef mem_view_contig_cython(double[:, ::1] M):
    cdef Py_ssize_t dim0 = M.shape[0]
    cdef Py_ssize_t dim1 = M.shape[1]
    cdef Py_ssize_t i,j
    
    for i in range(dim0):
        for j in range(dim1):
            M[i,j] = sin(M[i,j])    

    return M

Results

Comparison for matrix dim smaller/equal 100

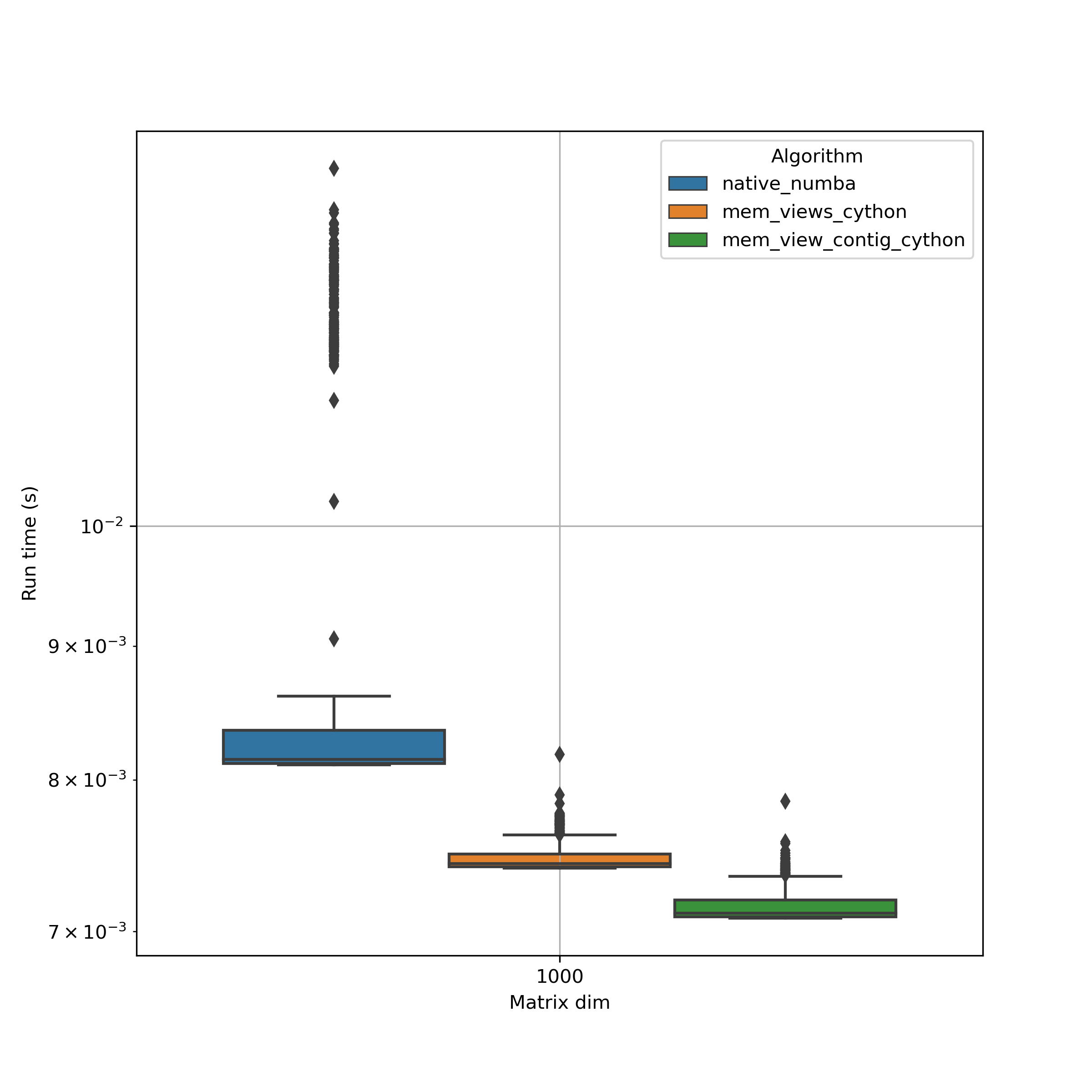
Comparison for matrix dim == 1000

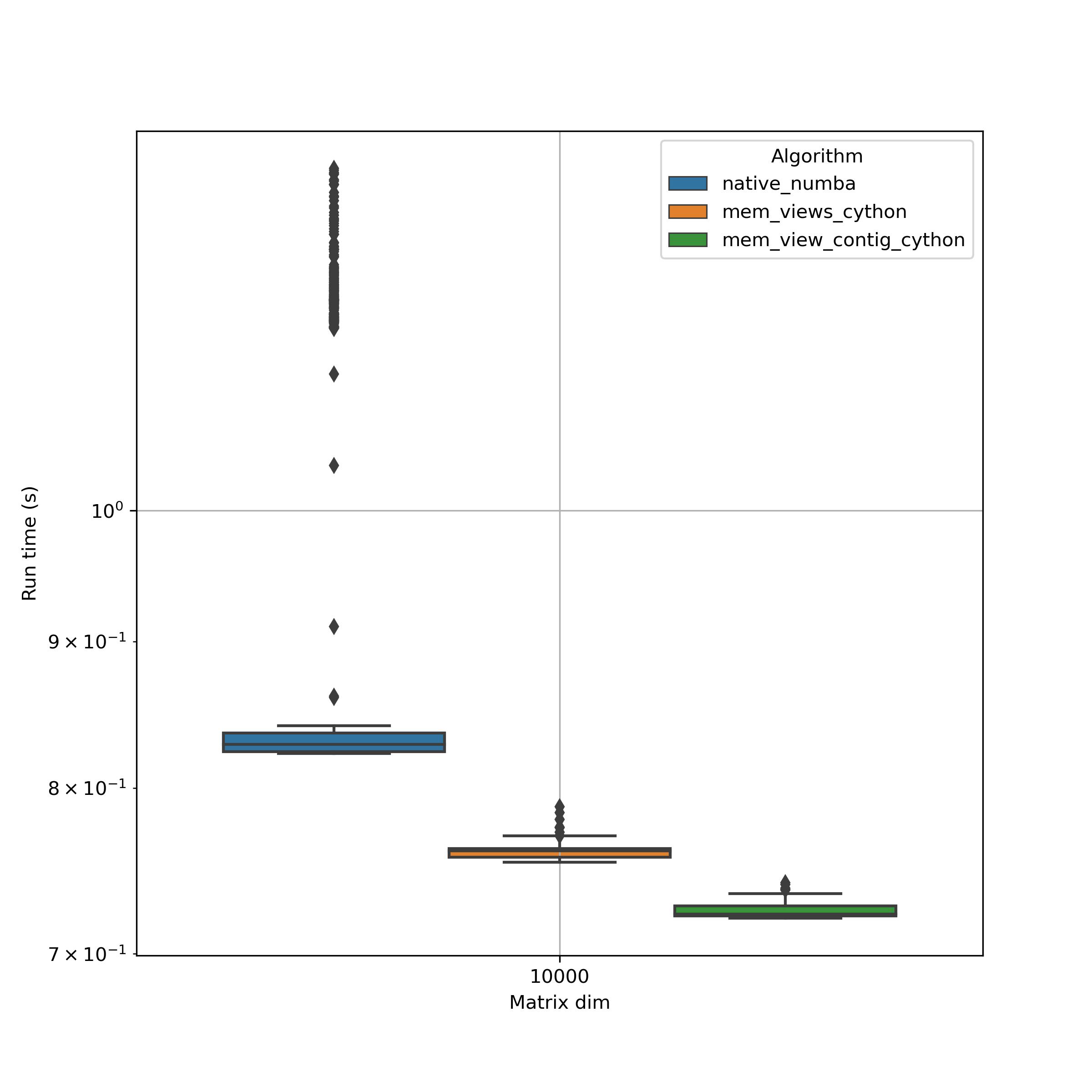
Comparison for matrix dim == 10000

NB!: Using np.sin(M) involves a few inefficient memory copies which make it basically useless for large arrays. It would be getting worse if used in combination with @numba.njit(parallel=True).

Conclusions

A key observation is the high variability when using numba. Optimized cython functions seem not only to be faster but the overall performance is more constant. This is extremely important for production use.

When we know the memory layout of a numpy array, then using contigous memory views are worth adding the :1 ;).